I need an exercise to learn the programming language Julia. I have used in in the past as a toy program to implement a finite-difference solver for seismic waves; but despite the reputation of the language (somewhat along the lines of as easy as MATLAB, as fast as C), I then found it to be rather hard, and not so straightforward to port my codes from MATLAB to Julia. It requires quite a bit more work to initialize appropriate dataformats, and I find that it’s not as easy to slice data in Julia as it is in MATLAB.
Anyhow, I decided to implement the Cagniard-de Hoop method following the theory of Jos van der Hijden. I have done this before in MATLAB, but then implemented the method in the general 3-D sense, to then only use it on 2-D wave propagation anyhow. The MATLAB code is alright, but can require up to 7 hours to compute appropriately accurate solutions, which is of course ridiculously long. I want to get this computational time down significantly, but the 3-D nature of the code actually prevents me from doing this (this has to do with the fact that it involves complex analysis along different branches, and the selection procedure to catch the appropriate branch in 3-D is prone to failures). I hope that a 2-D code can actually simplify matters a little bit.
On this blog, I’ll try and catalog my code as I write it. Any reader should refer to the dissertation of Van der Hijden for more details.
Bond transform matrix
This matrix allows us to rotate a stiffness matrix. Typically, the Bond transform is defined for the (6x6) stiffness matrix that applies in 3-D media. However, I simplify it for a (3x3) stiffness matrix, as applicable in 2-D media. It takes an input variable d, which is the angle (in degrees) with which the medium is rotated in the counterclockwise direction, assuming x pointing to the right and z pointing up. (Note that we typically assume z pointing down, in which case this transform thus results in a clockwise direction of the medium.)
# --- Bond transform matrix
function BondMatrix2D(d)
b = [cosd(d) cosd(90 - d);
cosd(90 + d) cosd(d) ];
# --- Let's be clever about this. Submatrix (left-top) is just the b^2
M1 = b.^2;
# --- Each column is the product of the 'other 2' colums of b
M2 = 2 * b[:, 2] .* b[:, 1];
# --- These are just determinants (but with + rather than - the crossed term)
M4 = b[1,1]*b[2,2] + b[1,2]*b[2,1]
# --- Output the 2D Bond transform matrix
M = [M1 M2;
-M2'/2 M4]
return M
end
System matrix ‘A’ and source vector ‘F’
Matrix ‘A’ contains the primary information about a medium; it must be constructed for each medium within our domain. The source vector follows similarly, and is computed here as the building blocks based on the matrix C are already present. Simplified for 2-D media (where C is 3x3, rather than 6x6), it may be computed in the following way, where I have explicitly written out all matrix-matrix operations, in the hope that this is faster and retains the symmetry of the system better… I used Wolfram Mathematica to simplify the 2-D expressions,
Inverse[{{C55, C53}, {C53, C33}}].Transpose[{{C15, C13}, {C55, C53}}] // MatrixForm // FullSimplify
{{C11, C15}, {C15,C55}} - {{C15, C13}, {C55, C53}}.Inverse[{{C55, C53}, {C53, C33}}].Transpose[{{C15, C13}, {C55, C53}}] // MatrixForm // FullSimplify
and then the matrices are computed as follows.
function AFmatrix(C,s1,rho,f,h)
DD = (C[2,3]^2-C[2,2]*C[3,3]);
CzziCzx = [(C[1,3]*C[2,2]-C[1,2]*C[2,3])/DD 1;
(C[1,3]*C[2,3]-C[1,2]*C[3,3])/DD 0];
CxxmCxzCzziCzx = [(C[1,3]^2*C[2,2]-2*C[1,2]*C[1,3]*C[2,3]+C[1,1]*C[2,3]^2+C[1,2]^2*C[3,3]-C[1,1]*C[2,2]*C[3,3])/DD 0;
0 0];
A1 = -s1 * CzziCzx;
A2 = inv([C[3,3] C[2,3];
C[2,3] C[2,2]]);
A3 = rho*I - s1^2*CxxmCxzCzziCzx;
A = [ A1 A2 ;
A3 transpose(A1) ];
F = [ CzziCzx*h[:,1]+h[:,2] ; f + s1 * CxxmCxzCzziCzx * h[:,1] ];
return A,F
end
Note, interestingly, how we used “I” to represent an identity matrix without specifying the size. I suppose this means that the resulting code can actually be run faster, as the meaning of the “I” operator is used, rather than its matrix representation. Clever.
Eigenvalue decomposition
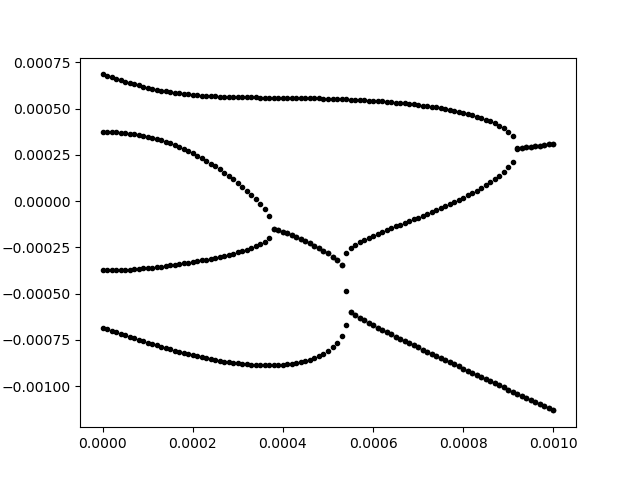
Next, we require the (repeated) eigenvalue decomposition of matrix A. Ideally, I can plot the results. This took me quite a while in Julia, as the plotting parameters are not in the slightest as comfortable as those in MATLAB. Eventually, I settled on using the PyPlot back-end. In this way, we can plot the slowness surface of a given stiffness matrix. For example, the following code that puts the ideas from above into practice may be run (ending on gcf(), to display the result within juno; the close() command that follows it is required to restart drawing, as the plot() command just writes on top of the previous result.).
M = BondMatrix2D(22.5)
C0 = [64 18 -4;
18 46 -2;
-4 -2 7 ]*3.1e8;
C = M * C0 * M'
rho = 2000;
s1=0;
f = [1;0]
h = [0 0; 0 0];
# === Get and sort D matrix (0th iteration, with s1=0)
using PyPlot
for s in 0:100
s1 = s/100000;
A,F = AFmatrix(C,s1,rho,f,h);
L,D = eigen(A);
plot([s1;s1;s1;s1],real(L),marker=".",linestyle="none",color="black")
end
gcf()
savefig("slowness_pyplot.png") # Saves the CURRENT_PLOT as a .png
close()
The resulting figure is as shown below, which is the correct solution (the horizontal axis of the plot corresponds to the slowness along the “X” axis; the vertical axis corresponds to the slowness along the “Z” axis.
Pairwise minimum
When given the two inputs s=[1 5] and l=[4.4 0.8], I want to be able to say that s[1] is closest to l[2] and that s[2] is closest to l[1] – simultaneously. This is what is accomplished by the following function.
function pairwisemin(s3,l3)
mins,idx = findmin(abs.( repeat( l3 , 1, 2 ) - repeat(transpose(s3),2,1) ) , dims=1 );
idx = [idx[1][1] idx[2][1]];
# --- If (3) unique values appear, return to the program
# if sum(idx)==3
return idx;
# end
# # --- If (<3) unique values appear, establish which value is missing >> This branch is never hit...?
# idx2 = sortperm(vec(mins));
# expectedvals = collect(1:2);
# deleteat!(expectedvals, sort(unique(idx)));
# idx[ idx2[ (2-length(expectedvals)+1):end ] ] = expectedvals[end:-1:1];
# println("Oops, Im here")
# println(s3);
# println(l3);
# pause()
# return idx;
end
Two further assorted programs
I don’t want to explain all parts, so just take the following.
function ds3ds1(C,D0,D0I,s1,N)
# Partitions of the stiffness matrix
DD = @views (C[2,3]^2-C[2,2]*C[3,3]);
CzziCzx = @views[(C[1,3]*C[2,2]-C[1,2]*C[2,3])/DD 1;
(C[1,3]*C[2,3]-C[1,2]*C[3,3])/DD 0];
CxzCzzi = @views [(C[1,3]*C[2,2]-C[1,2]*C[2,3])/DD (C[1,3]*C[2,3]-C[1,2]*C[3,3])/DD;
1 0];
CxxmCxzCzziCzx = @views [(C[1,3]^2*C[2,2]-2*C[1,2]*C[1,3]*C[2,3]+C[1,1]*C[2,3]^2+C[1,2]^2*C[3,3]-C[1,1]*C[2,2]*C[3,3])/DD 0;
0 0];
# --- The differentiated system matrix A
dAds = [-CzziCzx zeros(2,2) ;
-2*s1*CxxmCxzCzziCzx -CxzCzzi];
# ---
ds3 = transpose(D0I[N,:]) * dAds * D0[:,N];
end
And the following, which takes up the most computational time due to its need for an eigenvector/eigenvalue routine
function AssignEigenvaluesEigenvectors(C0,s1,rho0,f,h,s30e,s30)
A0,F0 = AFmatrix(C0,s1,rho0,f,h);
L0,D0 = eigen(A0);
posneg0 = sign.(imag( L0./s1 ));
negidx = @views pairwisemin( s30e[1:2], L0[ posneg0.==+1 ] );
posidx = @views pairwisemin( s30e[3:4], L0[ posneg0.==-1 ] );
posneg0[posneg0.==-1]=2 .+ vec(posidx);
posneg0[posneg0.==+1]= vec(negidx);
posneg0I= round.(Int, posneg0);
s30[ posneg0I] = L0;
D0[:,posneg0I] = D0;
return s30,D0,F0
end
Finally, the program
A call to CdH() runs the entire program.
using Plots
function CdH()
theta = 0;
M = BondMatrix2D(22.5)
C0 = [64 18 -4;
18 46 -2;
-4 -2 7 ]*3.1e8;
C0 = M * C0 * M';
rho0 = 2000;
C1 = 4.5*C0;
rho1 = 1.5*rho0;
# -------------------- Setup source details
f = [1;0]
h = [0 0; 0 0];
# -------------------- Setup receiver details
h0 = 200;
h1 = -300;
x = 10;
N0 = [3 3 4 4]; # P/ P/ S/ S/
N1 = [1 2 1 2]; # P\ S\ P\ S\
# -------------------- Setup temporal vector
ts = collect(0:2e-5:0.8);
solution1 = ts.*0;
# -------------------- Setup initial iteration details
A0,F0 = AFmatrix(C0,0,rho0,f,h)
L0,D0 = eigen(A0);
L0init = [-sort( -L0[ L0.<0 ] ); sort( L0[ L0.>0 ])]; # >> Sort as [-a1, -a2, a1, a2], with a1<a2.
A1,F1 = AFmatrix(C1,0,rho1,f,h)
L1,D1 = eigen(A1);
L1init = [-sort( -L1[ L1.<0 ] ); sort( L1[ L1.>0 ])]; # >> Sort as [-a1, -a2, a1, a2], with a1<a2.
# --- Julia-specific initializing of variables, so scope is kept
D0I = inv(D0); # Create for sake of Julia
# inve = transpose([D0[3:4,:] ; D0[1:2,:]]); # LinAlgebra version is faster than algebraic inverse
# facs = diag(inve * D0);
# D0I = diagm(0=> 1 ./ facs) * inve;
Fp = 1+im;
# -------------------- Start iterating
for N = 1:4
println(N)
s1new = 0;
s1 = 0;
s30c = complex(L0init);
s31c = complex(L1init);
s30 = complex(L0init);
s31 = complex(L1init);
for ii=1:length(ts)
t=ts[ii];
if t< ( L0init[N0[N]]*h0+L0init[N1[N]]*h1 )
continue;
end
s30h = complex(s30c);
s31h = complex(s31c);
s30c = complex(s30);
s31c = complex(s31);
s30e = complex(2*s30c - s30h); # Expected s3 (eigen)values (medium 1)
s31e = complex(2*s31c - s31h); # Expected s3 (eigen)values (medium 2)
jj=0;
while (abs(s1*x+s30[N0[N]]*h0+s30[N1[N]]*h1-t )>1e-10 || jj==0) && (jj<100)
s1 = real(s1new) + im*(abs(imag(s1new))+eps()); # Keep Im[s1]>=0
# --- Assign eigenvalues and eigenvectors to medium 1
s30,D0,F0 = AssignEigenvaluesEigenvectors(C0,s1,rho0,f,h,s30e,s30e);
s31,D1,F1 = AssignEigenvaluesEigenvectors(C1,s1,rho1,f,h,s31e,s31e);
D0I = inv(D0); # Faster than doing it algebraically
# --- Newton-Raphson iteration
s1 = s1 - im*eps(); # Correct for minor imaginary part
Fp = ( x + ds3ds1(C0,D0,D0I,s1,N0[N]) * h0 + ds3ds1(C0,D0,D0I,s1,N1[N]) * h1 );
s1new = s1 - ( s1*x + s30[N0[N]]*h0 + s30[N1[N]]*h1-t ) ./ Fp;
jj=jj+1;
end
# --- Scattering matrix
D1I = inv(D1);
Q = D1I * D0;
R = @views Q[1:2,1:2] \ Q[1:2,3:4];
BJN = D0[:,N1[N]] .* ( transpose(D0I[N0[N],:]) * F0 ) * R[N1[N],N0[N]-2] ;
dsdt = 1/Fp;
sol = 1/pi * imag( BJN * dsdt );
solution1[ii] = solution1[ii] + cos(theta)*sol[1] - sin(theta)*sol[2];
# if (ii%50==0)
# # println(ii)
# p = plot(ts,solution1);
# display(p);
# end
end
p = plot(ts,solution1);
display(p);
end
end